Some Ruggedness (DRS) Comparisons for Mountain Ranges

A natural question to ask is "is Mountain Range X more rugged than Mountain Range Y?" This is a bit of a slippery question, but ORS gives one way of answering such questions, by quantifying a certain measure of the ruggedness of a region.

We do this essentially by taking the average ORS value of each point in the region. This results in a measure of ruggedness, which we call domain relief and steepness (DRS), which rewards both relief and steepness. Click here for an old, but still valid, explanation of DRS. See the bottom of this page for acknowledgements.

NEW: Technical rough draft paper on RORS and DRS (ruggedness)

However, there is still the question of how large a region to select to represent the range in question, since ranges do not have precisely delineated boundaries. I have decided not to decide; rather, I present the data in graphical format, with ruggedness values calculated for various different versions of each range. (I also present tables below with the same data.) See below the first graph for a more detailed explanation of what these graphs mean.

NOTE: Most of these calculations use an old version of DRS (which we used to call simply "ruggedness", or "Rug"), which in turn used an old normalization of ORS (spire measure). The old version differs from the most recent version by up to 25%, in a way that depends on the steepness of the terrain. These DRS calculations remain qualitatively correct, but direct comparisons between these numbers and the ORS values for individual peaks are suspect. I plan to eventually update these DRS calculations to the new version of ORS.

NEW: A detailed workup of the Wasatch Range in Utah (using the most recent version of DRS)

A preliminary workup of Zion National Park in Utah (also using the most recent version of DRS)

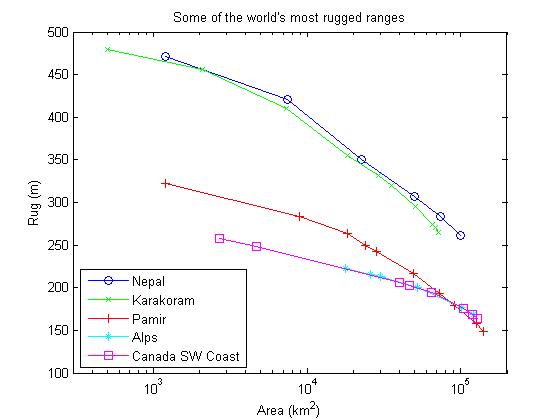
Here is a comparison of some of the world's most rugged ranges.

Nepal Karakoram Pamir Alps SW BC Coast

Click on the name of a range in the legend box to see pictures of some of the regions displayed on this graph.

Here is how to read this graph and the others like it on this page. For example, let's look at the Nepal Himalaya. The data point at Area = 99200 km^2, Rug = 261m, indicates that if we look at all the possible subregions of Nepal with area 99200 km^2, the most rugged such region has a ruggedness (roughly, average spire measure) of 261m. This is a rather large interpretation of "The Nepal Himalaya," as you can see by the picture here.

If we focus down to a smaller size, and still look for the most rugged region, the average ruggedness will increase, since we are picking the best parts of the larger region. So for example, the data point at Area = 50300 km^2, Rug = 307m, indicates a fairly restrictive interpretation of "The Nepal Himalaya," which excludes much lowland and plateau terrain. And the data point at Area = 7500 km^2, Rug = 421m, just selects parts of the Dhaulagiri, Annapurna, Mansiri, and Ganesh Himals, the very ruggedest parts of the Nepal Himalaya. At the left-hand extreme of the Nepal curve, the data point at Area = 1200 km^2, Rug = 471m represents just the Annapurna Himal, which turns out to be the ruggedest massif within the Nepal Himalaya, and probably the ruggedest massif in the world.

A similar story is true for all of the ranges on this graph and on all the graphs on this page: one can look at a large version of the range, encompassing everything one could define as being in that range, including much foothill terrain, but this will lead to a relatively low average ruggedness. Or one can look at smaller and smaller versions of the range, or subranges/massifs within the range, always selecting the most rugged region with a given size. These will have higher and higher average ruggedness as the size decreases, but they will be less representative of the range as a whole.

Further notes:

  1. Note that the area (x) axis uses a logarithmic scale.
  2. When the graph of one range (say the Karakoram) is always above that of another range (say the Pamir) then we can confidently say that the first range is more rugged. If the curves are close (e.g the Karakoram and the Nepal Himalaya) or cross each other, we can't judge one or the other as the clear winner.
  3. Some ranges are bigger in area than others; e.g. the curve for the Pamir stops around 30,000 km^2 since the range is simply smaller than some of the others. Also, for some ranges I have not calculated ruggedness values for all possible areas. Here, the calculations for A < 10000 km^2 focus on the best part of a range, or even the single most rugged massif.
  4. Although I have not put explicit error bars on the plotted points, a difference of less than 5% is never significant. Also, the lines between the data points are simple linear interpolation, so they are not very precise.

The next graph focuses on North America's best ranges.

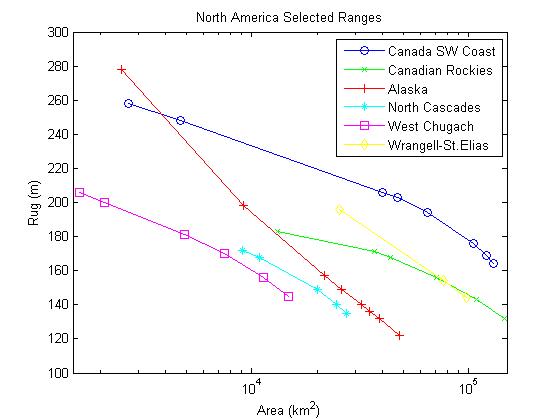
So-BC-Coast Canadian Rockies Alaska North Cascades West Chugach Wrangell-St. Elias

Click on the name of a range in the legend box to see pictures of some of the regions displayed on this graph.

Now we turn to the contiguous US---just a few selected ranges.

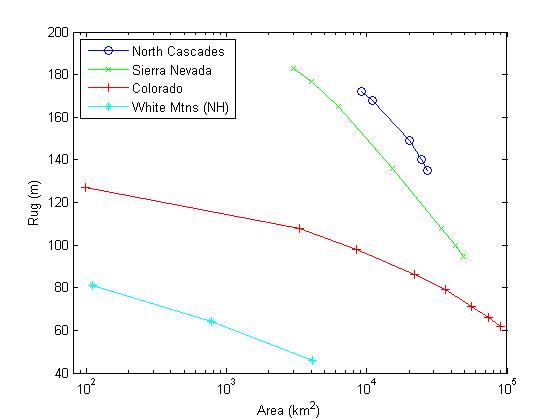
North Cascades Sierra Nevada Colorado White Mtns (NH)

Click on the name of a range in the legend box to see pictures of some of the regions displayed on this graph. (Not all data points have corresponding pictures.)

Here are another few selected world ranges.

New Zealand Norway Norway

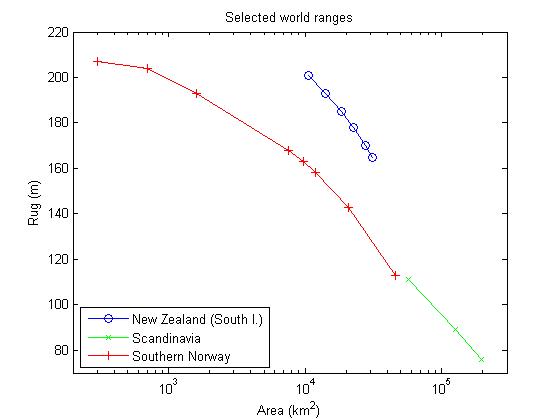
Click on the name of a range in the legend box to see pictures of some of the regions displayed on this graph. (Not all data points have corresponding pictures.)

One convenient way to see these comparisons is to choose some (arbitrary) sizes and compare at those fixed sizes.

Alps-size ranges, compared at 100,000 km^2
Range Ruggedness (m)
Nepal Himalaya 261
Southern BC Coast 178
Alps 177
Southern Canadian Rockies/Columbia 146
Scandinavia 92

Colorado-size ranges, compared at 50,000 km^2
Range Ruggedness (m)
Nepal Himalaya (Small) 307
Karakoram (Small) 297
Southern BC Coast (Small) 200
Alps (Small) 200
Southern Canadaian Rockies/Columbia (Small) 165
Alaska (Big) 120
Scandinavia (Small) 110
Southern Norway 110
Sierra Nevada (Big) 94
Colorado 72

North Cascades-size ranges, compared at 25,000 km^2
Range Ruggedness (m)
Nepal Himalaya (Very small) 345
Karakoram (Very small) 335 (rough)
Southern BC Coast (Very small) 225 (rough)
Alps (Very small) 216
Southern Canadian Rockies/Columbia (very small) 175 (rough)
Alaska 150
North Cascades 140
Southern Norway 135
Chugach 140
Sierra Nevada 125
Colorado 84

Western Chugach-size ranges, compared at 12,500 km^2
Range Ruggedness (m)
Karakoram (Hunza Valley plus some extra) 380 (rough)
Alaska (Small) 190
North Cascades 164
Southern Norway (Small) 156
Western Chugach 152
Sierra Nevada 142
Colorado 95

Acknowledgements: Ruggedness is based on spire measure; see the main spire measure page for the relevant acknowledgements. Ruggedness itself was developed by David Metzler and Edward Earl. All ruggedness calculations on these pages are by David Metzler.

Questions and comments welcome:

metzler (at) aa (dot) edu